
A Summary of the Lessons & Juicy Book Details Quick Links
Here’s a helpful summary of everything that is covered throughout this page. You’ll find plenty of images and details for the book, but there are also some very valuable lessons and tips to be learned about dynamic symmetry and the golden section (phi). Enjoy!
- Cinematic Book Preview Video
- Dynamic Symmetry Book: What’s Inside?
- Why Dig Deeper?
- Where to Start?
- Understanding the Reciprocal
- A 3rd Grader’s Calculator
- Think Like an Egyptian
- Dynamic Symmetry & Golden Section Connection
- Why the Ratios are Gold
- 240 Dynamic Symmetry Grids and How They are Applied
- Book Table of Contents
- How the Book Cover & Abstract Letters were Designed
Book Preview Video Dynamic Symmetry
Back to Summary
This is a cinematic book preview, which was captured by using a configured root 6 rectangle that is demonstrated on the dynamic symmetry grid page. The printed version from Amazon is displayed. They did an amazing job on the printing…the images are crisp, clear, and have a shine to them.
Please enjoy the video and share it if you want to help change the future of art. Subscribe on YouTube if you’d like to see more videos. Thank you!

DYNAMIC SYMMETRY BOOK What's Inside?
Back to Summary
Serious visual artists can now easily understand and apply the secret geometry that masters used to create remarkable art. Superior mathematical skills aren’t required because there are hundreds of excellent step-by-step diagrams to explain everything with simplicity. Learn how the ancient and modern masters used dynamic symmetry to promote unity, movement, rhythm, and strength. These qualities, along with many others, allowed their art to have visual clarity, impact, and stand the test of time. This is an essential book for painters, photographers, sculptors, and cinematographers that hold composition and design with a high priority.
For far too long, artists have been stuck with the basic tools of artistic composition, like the rule of thirds and leading lines. Unfortunately, we’re incapable of reaching the master level if all we know are the basics. Powerful tools like dynamic symmetry and other composition techniques have been kept a secret from all of us. It’s time to learn of them, push past any plateau that stands in our way, and finally unlock our true potential!
FOR PRINTED VERSION
Looking for a printed version? Please go to Amazon for a beautiful softcover or hardcover!
Every purchase helps support this site to bring more free videos and articles to artists that are wanting to master composition. It is much appreciated!
The Book Includes:
1. 26 chapters
2. 500 pages from front to back
3. Over 900 step-by-step diagrams and photos
4. Content for painters, photographers, cinematographers, and sculptors
5. Basic to Advanced knowledge of Dynamic Symmetry
6. Download Size: 1.33GB
7. Table of contents further below with more info
After purchasing the book from the store, you will be directed to the download page and you’ll also receive an email with the link. On a MOBILE DEVICE? No worries! With the link in the email, you can get the goodies when you’re back at your main computer.




Why Dig Deeper? Dynamic Symmetry
To Summary
Dynamic symmetry is the foundation of masterful art, it’s true, but why would another book need to be written on the subject?
That’s a great question, and it can be answered with two words; visual artists.
Most books that have been written about dynamic symmetry are based on the assumption that everyone has a great understanding of math. Unfortunately, most visual artists struggle to cross the bridge from the creative, to the logical side of the brain. At least that was the case for me! That’s what the book “Dynamic Symmetry: The Foundation of Masterful Art” remedies. It bridges the vast gap and allows visual artists to understand and apply the same powerful geometry that the masters of the past used in their art.
There are plenty of reasons why a new book needed to be made, but let’s cover a few key points real quick, then move on to some interesting lessons (more details for older books).

Don’t get me wrong, each dynamic symmetry book from the past is great in one way or another. Even if they can’t be fully understood by visual artists, it still leaves bread crumbs for them to follow until a bridge of understanding is created.

The Elements of Dynamic Symmetry
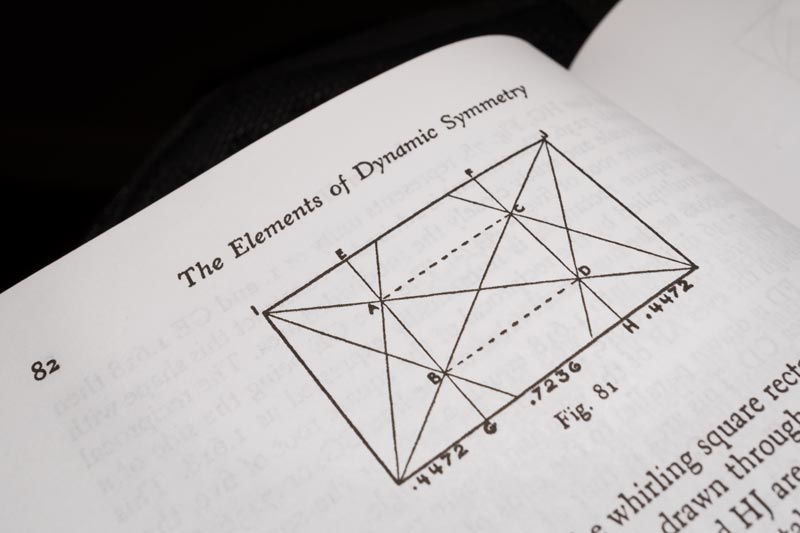
Here’s an example from the book “The Elements of Dynamic Symmetry” by Jay Hambidge (1920). It’s an excellent resource for math savvy individuals, but the visual artists are left slamming their heads against the wall trying to decipher the message and use it in their art.

There was one section in Hambidge’s book that completely had me stumped (Lesson II). He was using a grid with several letters and trying to teach how to subdivide the rectangle by using the grid. None of it made sense…at first. I must have cried six times, pulled my hair out twelve times, and read it twenty times before an inkling of understanding was made.
Slowly but surely I cracked the code, understood it, then figured out how to teach it simply…in a visual way. Then, of course, I had to take it ten steps further! I knew that visual artists of the world needed to be able to understand dynamic symmetry in a simple way if they were going to use it efficiently in their art.
The Art of Composition: A Simple Application of Dynamic Symmetry
In this next example, we see pages from “The Art of Composition: A Simple Application of Dynamic Symmetry” by Michel Jacobs. Again, another great book which actually attempted to attract visual artists rather than mathematicians, but it fell short in a few ways.
The symbols created for each rectangle are more confusing than just using a simple shape like a square. Most of us are familiar with the square, right? So if we say that an image was composed in a root 4, which has a ratio of 2, it might be easier to compare the rectangle to two squares rather than a squiggly dashed line as seen on the left.
We’ll learn more about dynamic symmetry basics in the “Where to Start” section to follow.
Also, the black and white line illustrations weren’t masterful examples that could truly show the power of dynamic symmetry. Michel’s book was written in 1926, and Hambidge’s book in 1920…almost 100 years ago. We were definitely in need of a serious update! It’s time to include some digital photography, cinematography, and colorful, masterful examples!

The Painter’s Secret Geometry: A Study of Composition in Art
Another notable book for artists that can create confusion is “The Painter’s Secret Geometry: A Study of Composition in Art” by Charles Bouleau. This was a rare book for a while, but was republished in 2014. It’s exciting to have such a rare book available again, but some may find that it lacks the instructions for real-world application.
It’s 25 years of analytical notes collected by Bouleau, but it’s more math, plus the way it reads has an airiness to it. Almost like he wrote it to show how clever he was, rather than giving the artist valuable information for understanding composition and design.
Alas, it’s still a bread crumb that leads serious artists in the right direction.

Where to Start Dynamic Symmetry
Back to Summary
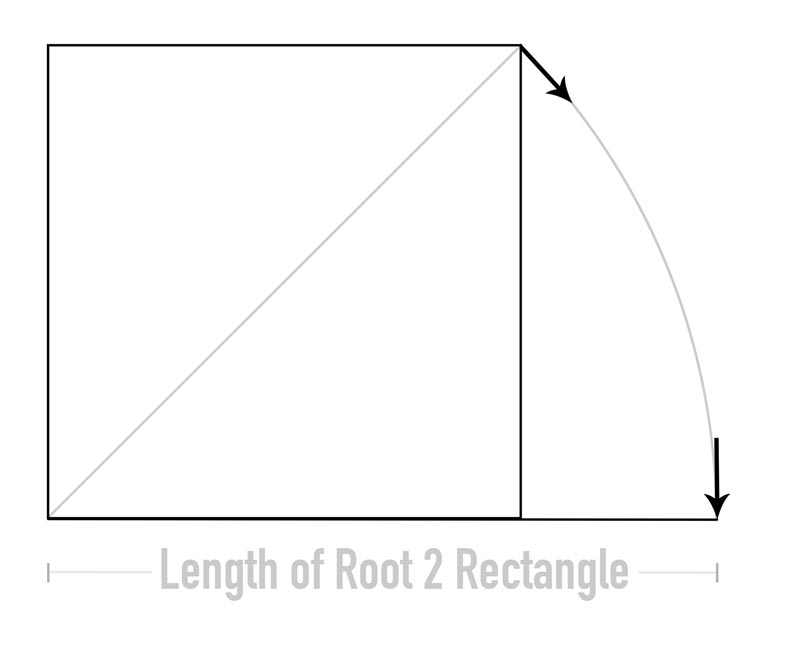
Most of us are familiar with the basics of dynamic symmetry, and the way the root rectangles are built. We swing the diagonal down from the square to create the root 2 rectangle. Then we swing the diagonal of the root 2 down to create a root 3 rectangle. And so on, and so forth.
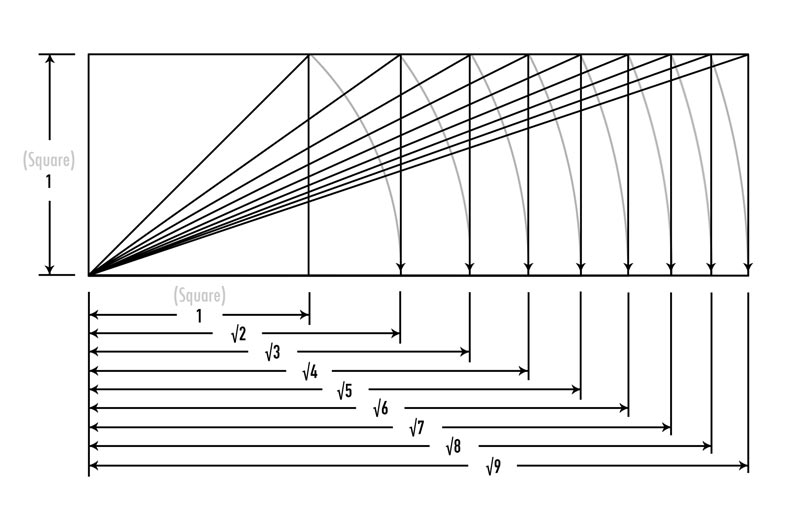
If this is your first time learning of dynamic symmetry, that’s how easy it is to build the root rectangles. The example below shows how the square is the starting point for every root rectangle.
Here’s a look at root rectangles one through nine being constructed by swinging a diagonal down and completing the rectangle. In the book, you’ll also learn how to create the other rectangles in this way, like the 5/4, 4/3, 1.5, Root Phi, and Phi.
The difficult thing to understand, though, are the ratios. If you’ve thumbed through “The Elements of Dynamic Symmetry” by Jay Hambidge, you might’ve seen all of the ratios he lists. How did he come up with these? What does the ratio of phi mean to visual artists? What do the other ratios mean to visual artists?
So many questions are unanswered because there’s only room for confusion when there’s not a bridge from math to visual. Let’s bridge the gap!
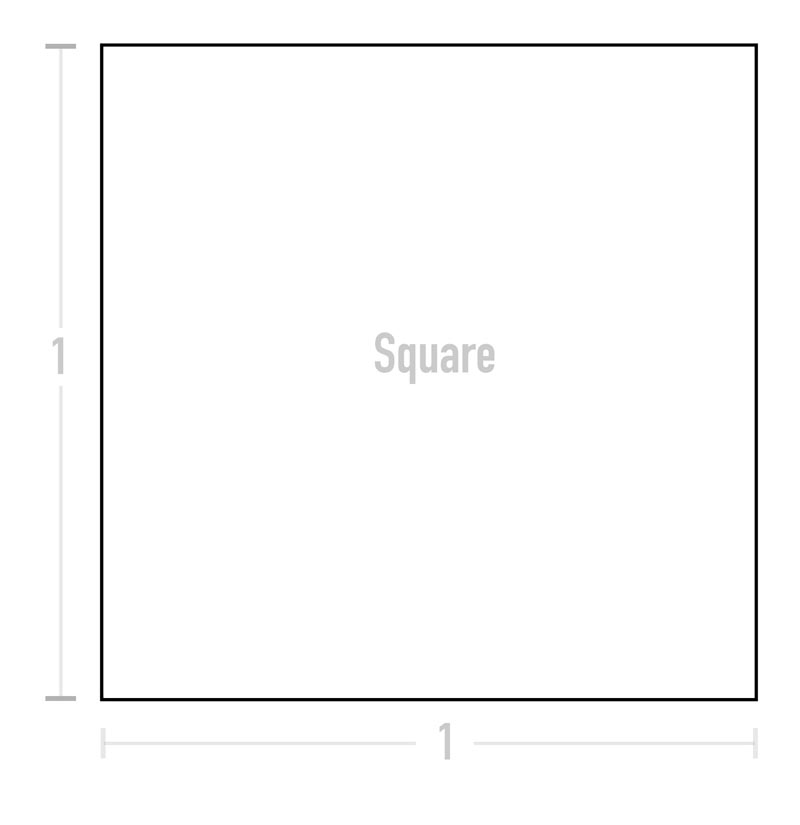
First, let’s take a look at what the ratio means visually. Instead of using different symbols to represent each rectangle, or scaring visual artists away with confusing ratios, let’s try the simple approach.
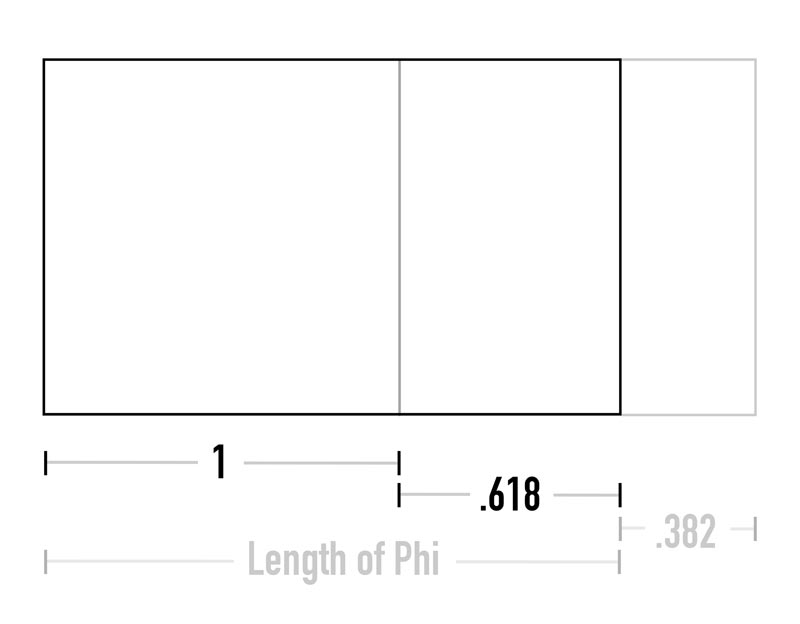
So, what do these mysterious ratios represent? Well, the ratios are merely a numerical representation of how many squares we see. Since we see only one square in this next example, the ratio is one. It’s a visual unit of measure, and since we all know what a square looks like, understanding the ratios is going to be a cinch.
When we look at the next diagram, we’ll see how we get the ratios by reading the length of the squares. Two squares equals the ratio of two. It doesn’t get easier than that!
The left side always remains one, but the length will change depending on the squares. This can be full squares or partial squares, but the important thing to remember is the way the ratio relates to the length of the shape (from left to right).
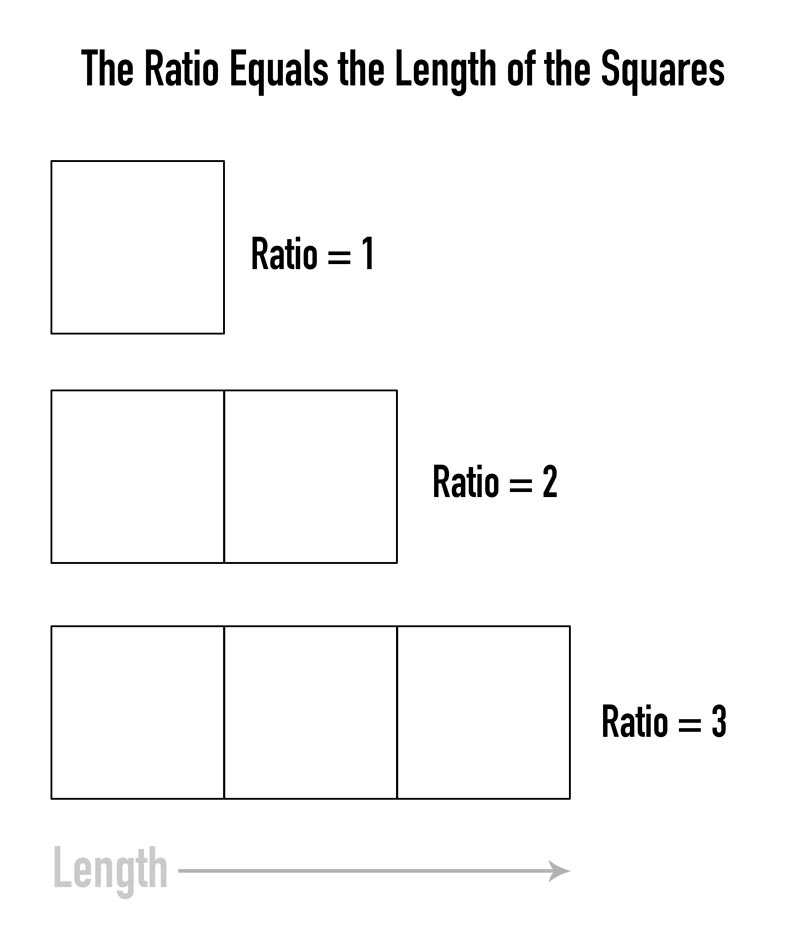
If we align the 1.5 rectangle to two squares, we’ll see that it’s only one and a half squares long. That’s where it’s ratio comes from.
The 1.5 rectangle has the same ratio as most camera sensors and canvases, so this is an important rectangle for both painters and photographers.
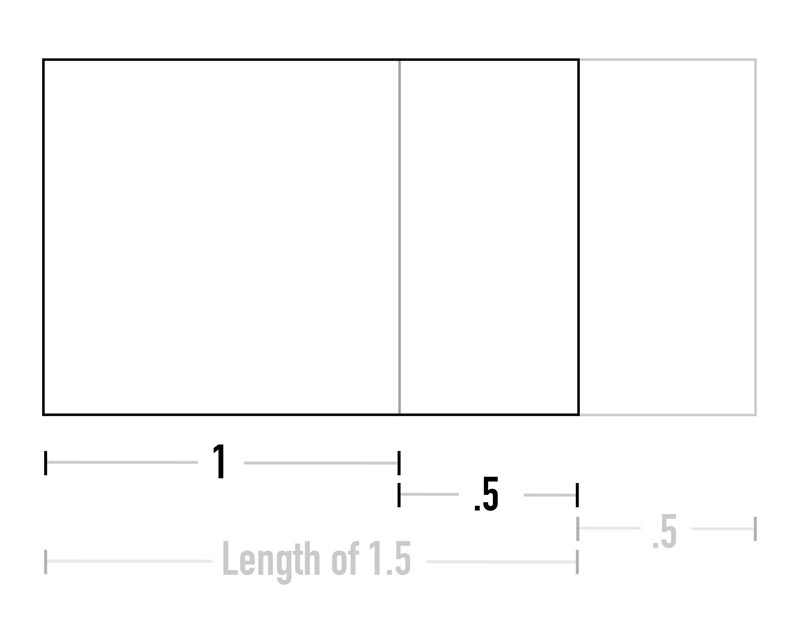
All of the rectangle ratios are read this way…compared to the square. In the next diagram, we can deepen our understanding of the ratio by simply adding and subtracting the shapes relating to the square.
We have the 1.5 rectangle, which is a square and a half, so when we subtract a square we are left with half of a square. Super simple, but bridging the gap for visual artists.
Now, when we add half of a square to the 1.5 rectangle, we get a total of two squares. Two squares actually equals the ratio of a root 4 rectangle!
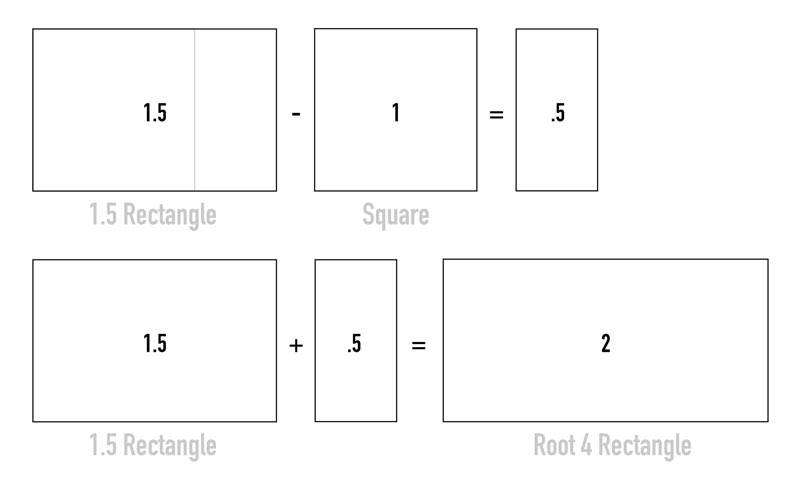
Now that we know how the ratios are seen visually, we know that the phi ratio of 1.618 is a little longer than one and a half squares, but less than two squares. That’s why we see the remainder of the two squares. This remaining portion of the second square has a length/ratio of .382. The simple math side of things looks like this: 2 – 1.618 = .382. Nothing a 3rd grader’s calculator can’t handle!
Understanding the Reciprocal Dynamic Symmetry
Back to Summary
When visual artists study dynamic symmetry, it’s important to fully understand the reciprocal of a rectangle. After all, if it’s not clearly understood we can’t use it to construct a new grid to fit our next masterpiece.
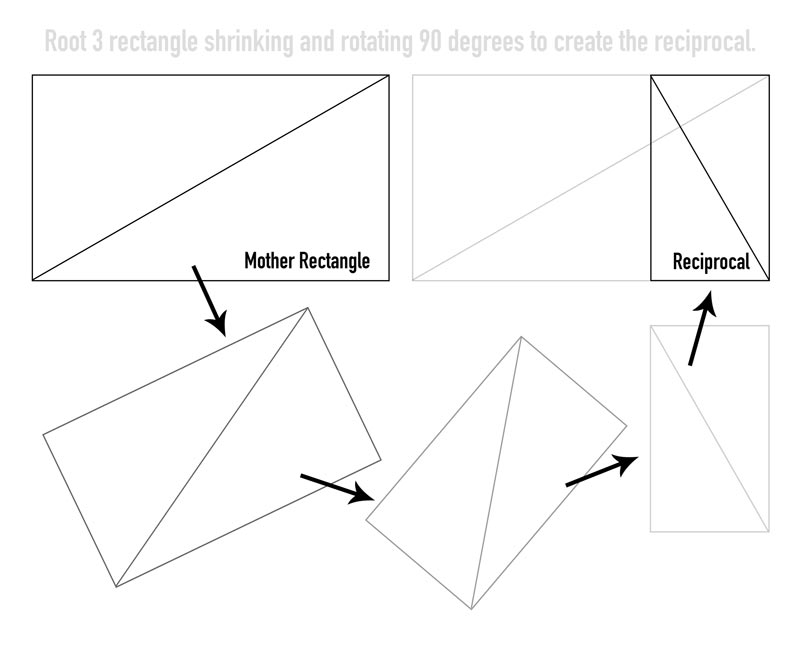
The reciprocal is confusing at first when it’s explained with numbers and geometry, but let’s look at it visually. To easily construct the reciprocal diagonal, let’s first draw the major baroque diagonal, which runs from the lower-left to the upper-right corner of the rectangle. We call it a “major” diagonal because no other diagonal can be drawn longer than corner-to-corner.
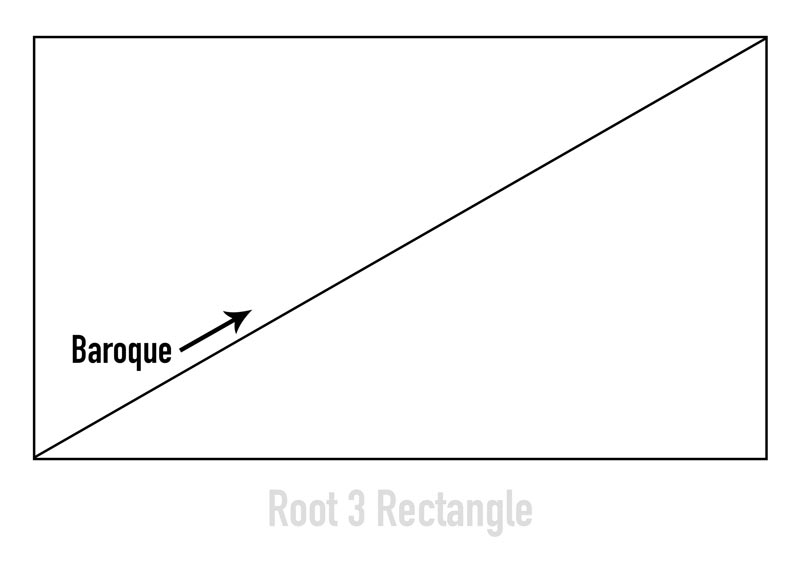
After the baroque diagonal is drawn, finding the reciprocal diagonal is easy. All we have to do is draw a line from the lower-right corner and make it intersect the baroque diagonal at 90 degrees.
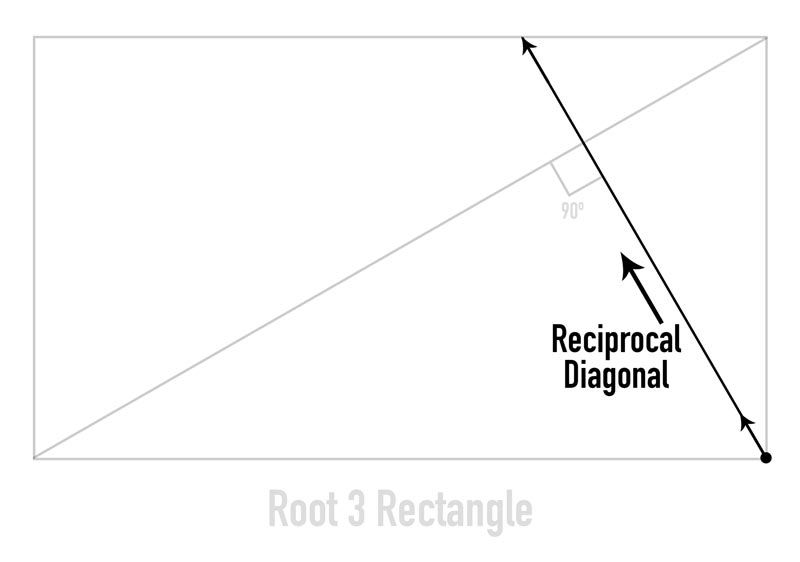
When ever we see an intersection of lines or where a line meets the edge, we get new “eyes” that we can generate more lines from. Creating lines from new eyes allows us to adhere to the geometry within the rectangle.
To demonstrate this, we can drop a line down from the eye that was created from the reciprocal diagonal meeting the top edge.
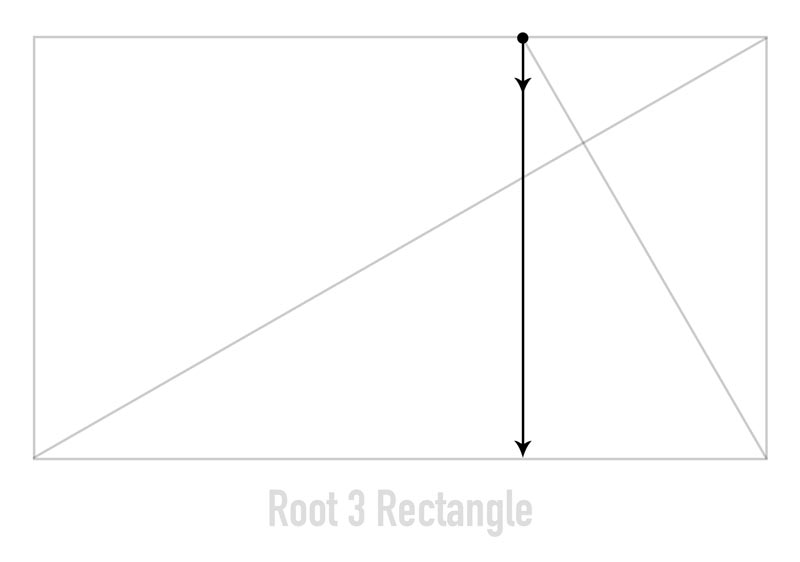
Once the line is dropped, we’re able to complete the reciprocal shape. And guess what? The reciprocal shape is exactly the same shape as the mother rectangle. Since we’re working with a root 3 rectangle, the reciprocal we just created is a smaller root 3 rectangle with the same proportions. Only, it’s smaller and rotated 90 degrees.
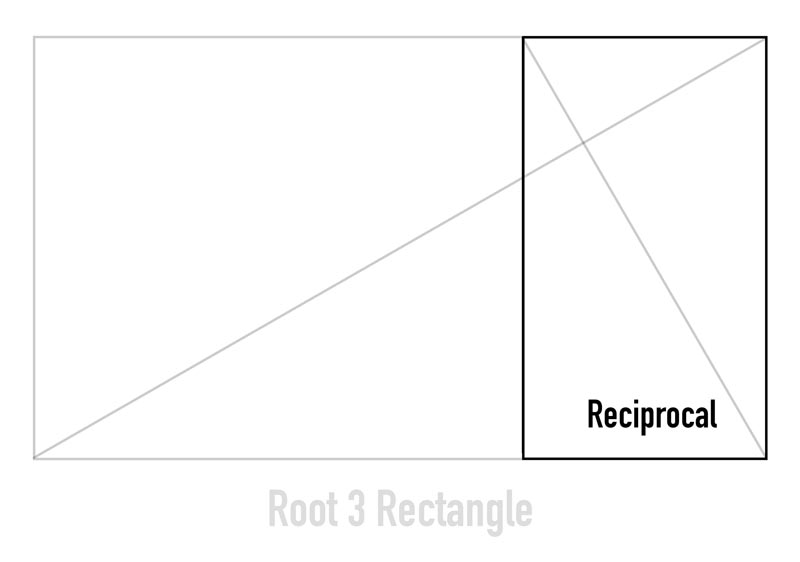
To understand what is going on visually, let’s take a look at this next animation. Basically, the reciprocal is nothing more than the mother rectangle rotated 90 degrees, shrunk down, and placed inside.
That’s why it is important to intersect the diagonal at 90 degrees. If we didn’t do it exactly at 90 degrees, we wouldn’t create a smaller rectangle with the same proportions.
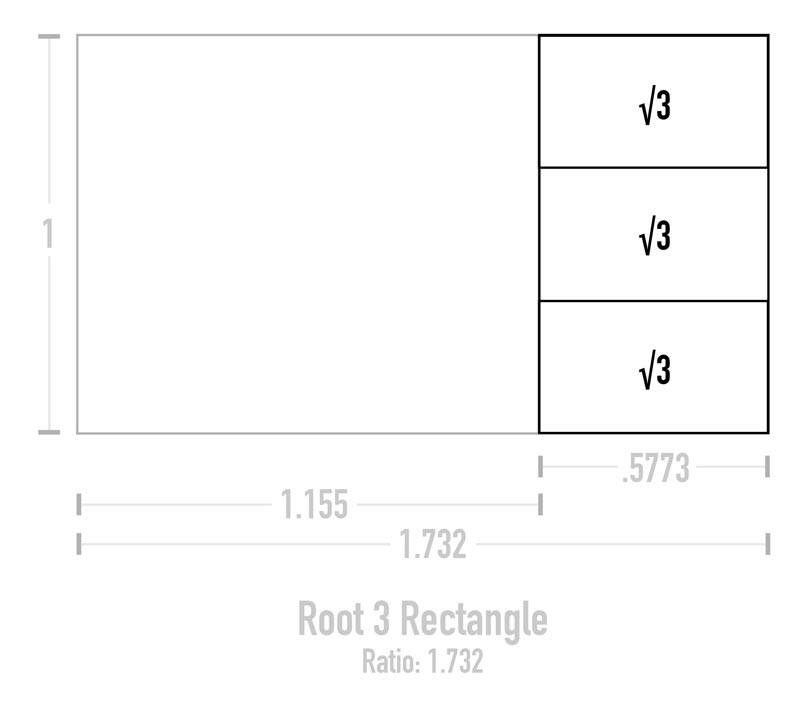
As we learned in the “Where to Start” section, it’s easier to understand the rectangles by reading the length from left to right and comparing them to the square. This means our reciprocal has the same left edge as the mother rectangle, which is equal to one. Therefore, the ratio of the reciprocal is going to be shorter. It’s ratio is .5773, so visually it is a little longer than 1/2 of a square.
We can then create a reciprocal within the reciprocal and get the same exact root 3 shape, yet smaller. All we have to do is keep intersecting the major diagonal at 90 degrees, then drop the line from the new eye to complete the shape. The book explains even more and shows how the root and phi rectangles can break down into various themes that will fit the needs of any artist.

AMAZING WORDS FROM ARTISTS AROUND THE WORLD!
Hello Tavis:
As you know we have had significant rainfall here in California (Joshua Tree National Park). The desert bloom is epic to say the least. The beauty of nature never ceases to astound me.
So, I took friends to my secret spot at the Park. Secret in that almost no one goes to this spot even though the rock formations are beyond description.
While there the lines and forms from dynamic symmetry stood out so clearly that I knew I had installed some of this magic into my brain.
On two occasions I shared what I was seeing with my friend who quickly saw the lines I had offered to him. In both cases he saw the 90 degree intersection that became the eye of the image. He knew some of this stuff even though it was apparent he hadn’t studied dynamic symmetry as such.
My reason for sharing these episodes with you is to thank you! Thank you for helping me to organize and utilize what I think and believe is inside our brains but doesn’t register until those gifts are made aware to us by people like you!
You sir have changed my thinking for composition in huge ways. Great ways at that! Thank you, thank YOU!
All the best,
Jeffrey Littell
Costa Mesa, CA
*****
Hi Tavis, hope all its going great!
I Just watched the video .. oh Thank You so much!! I really appreciate that you did this for your fans, and i am so happy, i win what i wanted !! haha.. i was trying to do some digital grids on my own but i’m not that good..
Anyway, i finally finished your book, it was a slow read since i basically draw on paper almost all the grids to be sure to not miss anything.. i really understand now where i was wrong, i’ts the most accurate book i ever read about composition.. and i hope to improve a lot in the next big piece of art i do, of course i am sure to grab new important information from your upcoming critique video!
Thank you very much again.. Hear you soon!
Gianfranco!
*****
Hi Tavis, Your teachings are giving my photography life. It’s absolutely amazing and its making me getting deeper into the art. I am absolutely grateful, and I will support your endeavors for as long as you create education/content. Thanks again sir for your contribution to the world, it is truly appreciated.
Gratefully,
Remi Goguen
*****
Hey Tavis, greetings from Berlin. I bought your phi grids and I use them in Photoshop. I also have read your book. Its great work and you opened my eyes for a great “new” way of creating images. Its especially helpful for my digital artworks and I also use it in advertising visuals, which makes them far better than before, were I only trusted my eye.
Thanks a lot for everything. Have a nice week.
Best,
Rüdiger
*****
Sir, today I am sending a different personal story to you and i intend to reveal before people in time. I at first saw the free videos of Myron Barnstone and then I discovered you. I got a treasure; DYNAMIC SYMMETRY. Your free videos gave me a direction for which I started development in my photography. Since 2018 I got 5 editors choice and most inspiring is that one of my photo had been published in National Geographic Your Shot. For this achievement if I thank any earthly person they are late M.Barnstone and You. Thank you Sir.
Nikhil Brahma
*****
*****
Tavis, thank you for your composition videos it has taken me to the next level of photography. I keep going over them from time to time because I seem to learn more from them each time.
It has been pretty cold here in the northeast but as soon as the weather breaks I am going out to start using what I have learned from you. Keep up the great work.
Art Romano
*****
A 3rd Grader's Calculator Dynamic Symmetry
Back to Summary
Math is one of the worst four-letter words for many visual artists, but it doesn’t have to be. Many 3rd graders already possess the mathematical skills to take advantage of the advanced dynamic symmetry lessons. Multiplication, division, addition, subtraction, simple fractions…it’s all any visual artist needs to know. Even if you don’t know how to write it out or do it in your head, a simple calculator does. Let it crunch the numbers for you!
Most of us have calculators on our phones, which is great! Just open your calculator app and it should look similar to the example below. If you rotate the phone into horizontal mode, you’ll get more options. We can use three of these buttons (reciprocal, squared, root) plus the standard buttons to zoom us right into the master level of understanding dynamic symmetry. No kidding!

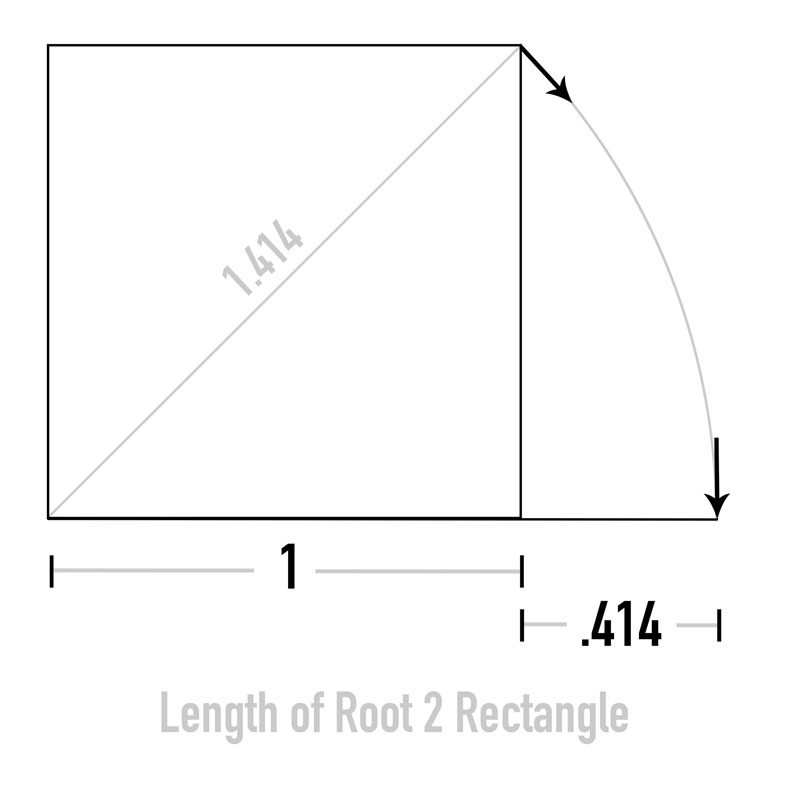
Want to quickly find the ratio of the root 2 rectangle? Just press the number “2” then the “root” button and you’ll get 1.414213562…but can be “rounded” to 1.414. When the number is rounded, it just means it is simplified…instead of showing a long string of numbers. The phi ratio of 1.618 is rounded because it actually goes to infinity.

Here’s a visual example of what happens when the number “2” and the “root” button is pressed. We swing the diagonal down and get the length/ratio of the root 2 rectangle.
If you’re wanting to find the reciprocal of the root 2 rectangle, just type the ratio 1.414 and press the “reciprocal” button to get .7072. If you push it again while .7072 is typed in, you’ll get 1.414 again. What that button does, is divides the number one by whichever number is typed. So visually, what the reciprocal button does is rotates the shape 90 degrees every time it’s pushed. In the book, we’ll see how this button visually helps us find the phi ratio with any number.

The “squared” button isn’t used as much until Chapter 19, where we learn how to construct the Great Pyramid of Giza, then use the Pythagorean theorem. It sounds crazy difficult, but it’s explained in a super simple way.
The squared button basically just multiplies whatever number is typed into the same number. So if the number ten is typed, it will multiply 10 x 10 to equal 100.

As you work through the book or build your own grids, keep your calculator nearby and it will tremendously advance your understanding of dynamic symmetry. You’ll be able to figure out the subdivisions of certain grids, while also designing your own like the one below.
You can even check out this video playlist to see how simple math can help construct the grids. Math is scary for visual artists, it’s true, but when it’s only at a 3rd grader level AND we can use a calculator, it becomes our friend.
“Without mathematics, there is no art.” Luca Pacioli


Think Like an Egyptian Dynamic Symmetry
Back to Summary
The Great Pyramid of Giza was built around 2584 B.C., so the Ancient Egyptians didn’t have iPhones and laptops to help them design their structures. What they did have, though, was basic geometry. Some may even refer to it as sacred geometry.
They were quite familiar with squares and circles, and used them for many things…including the design of the pyramid. Even if they weren’t aware of simple multiplication, division, addition and subtraction by using their basic shapes, they could still use a compass and a straight edge to design the pyramid. All they would have to do is start with a straight line.
Let’s draw a perfect square using basic tools to see how simple it is. We can start to recreate the design plans, where the square represents the base of the pyramid.
Start by drawing a line on a piece of paper. Any length will work.
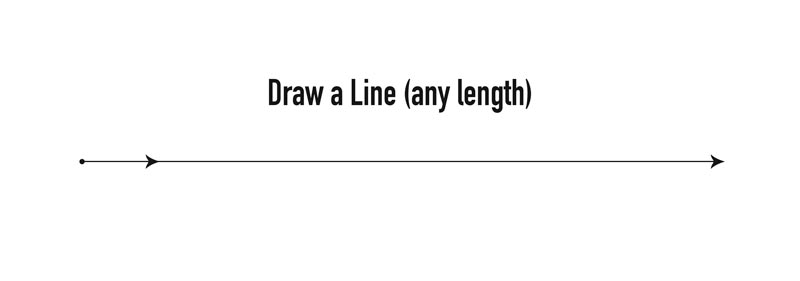
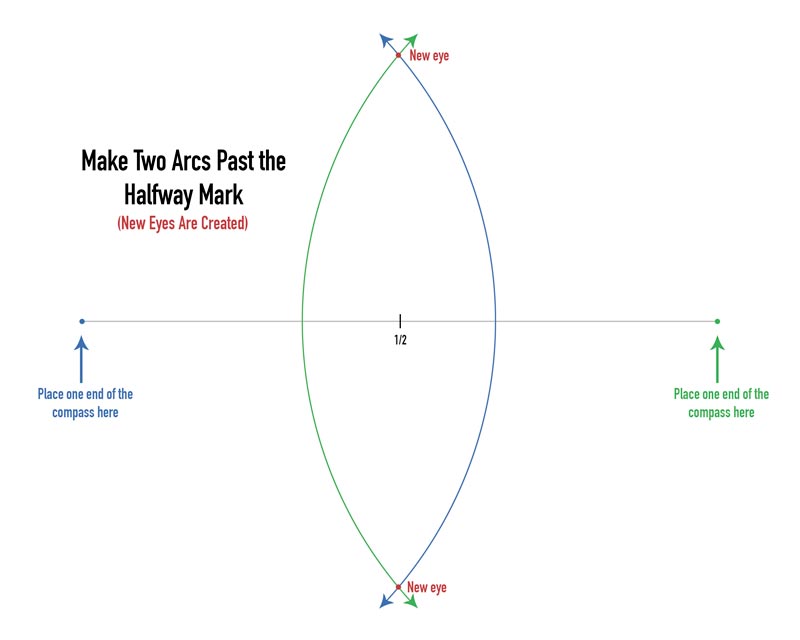
Next, take your compass and open it wide enough to draw an arc past the halfway point. In the diagram, you’ll see that the pointed end of the compass goes at the end of the line, then the pencil will draw an arc. Do this from both ends of the line, ensuring to cross the halfway point.
Notice that the arcs create new intersection points, or “eyes,” that we can generate a new line from. We can create new eyes in our dynamic symmetry grids as well, which is covered extensively in the book.
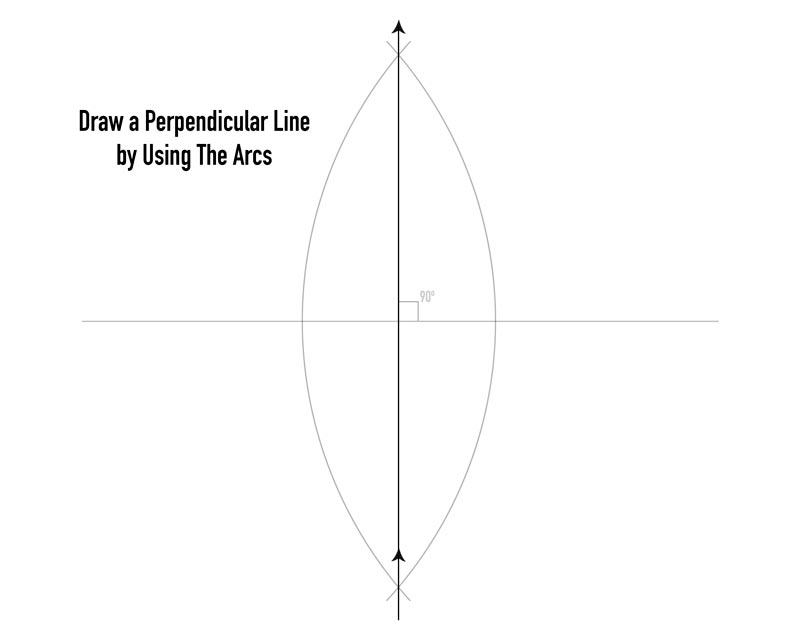
Draw a straight vertical line by using the eyes of the arcs. This creates a new line that is 90 degrees, or perpendicular, to the first line.
Place the pointed end of the compass right in the center eye and draw a circle. What this circle is doing, is creating four new eyes to generate new lines from.
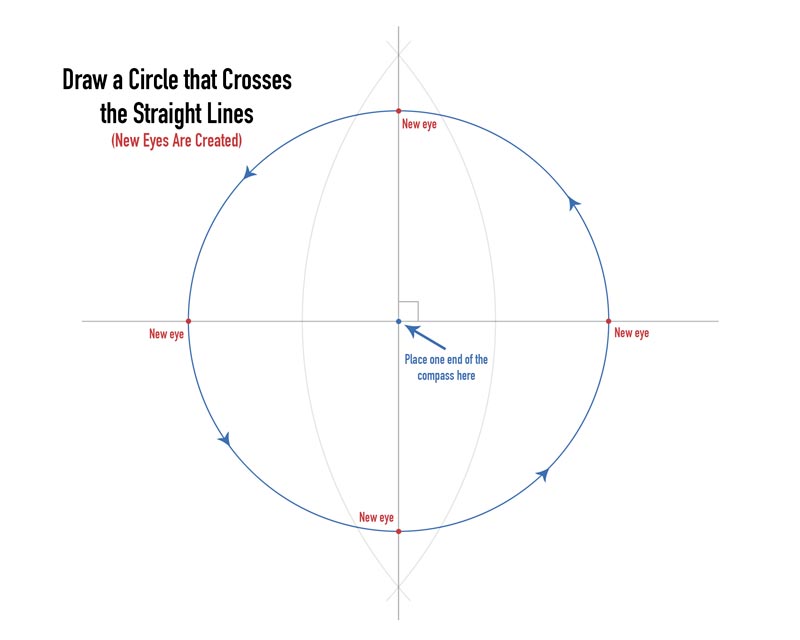
The perfect circle created four eyes that were equal distance from the center. Now all we have to do is draw a straight line from one eye to the next and we’ll get a perfect square.
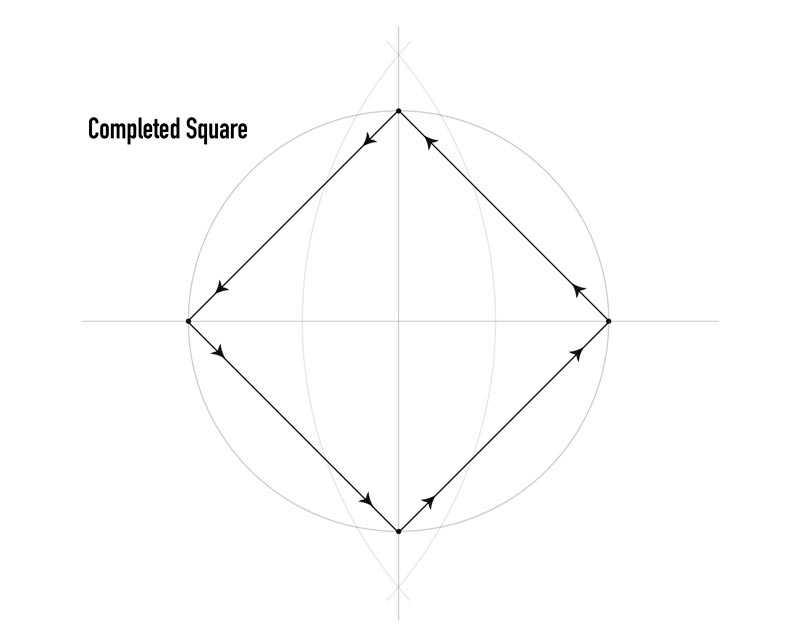
As you just learned, drawing a perfect square with a simple tool was surprisingly easy. We can design the construction plans for the Great Pyramid of Giza in the same way. And the extremely cool thing is that it all relates to dynamic symmetry!

In the book, you’ll learn how the root phi rectangle was used to construct the pyramid. The other circles and squares shown help construct the base, as well as geometric measurements that were thought to have brought them closer to their Gods.
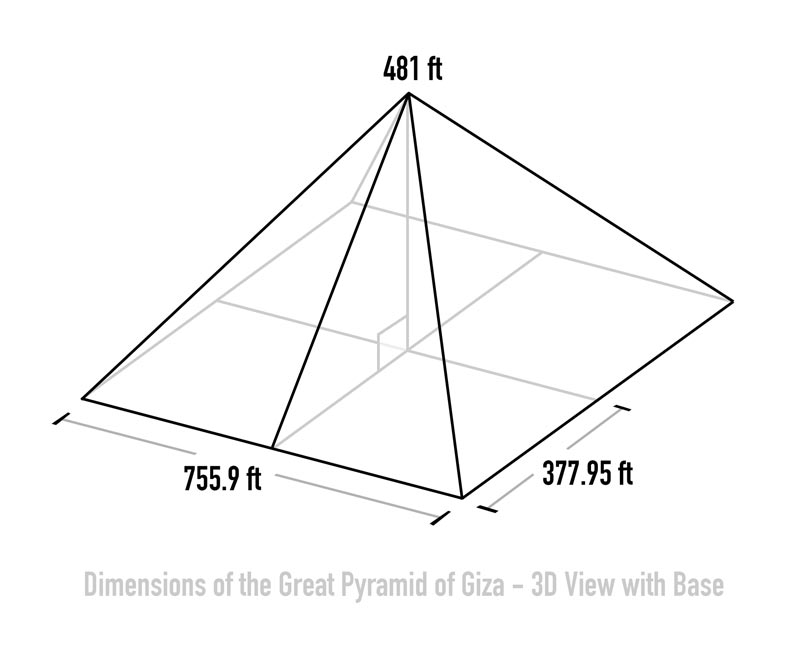
The way dynamic symmetry relates to the pyramids and its measurements is excitingly interesting and shows how every masterpiece starts with a solid foundation.

Whether we are creating a pyramid or a drawing,
we construct all masterpieces in the same way;
by starting with a strong foundation.

Golden Section Connection Dynamic Symmetry &
Back to Summary
As many artists know, the phi ratio has several different names like the golden section, golden cut, golden mean, divine proportion, etc. It also has many different visual representations which are seen in the next diagram.
As you work through different dynamic symmetry grids and ratios, you’ll start to notice that some are very similar to phi. Let’s have some fun and make note of the most interesting characteristics and relationships among them!
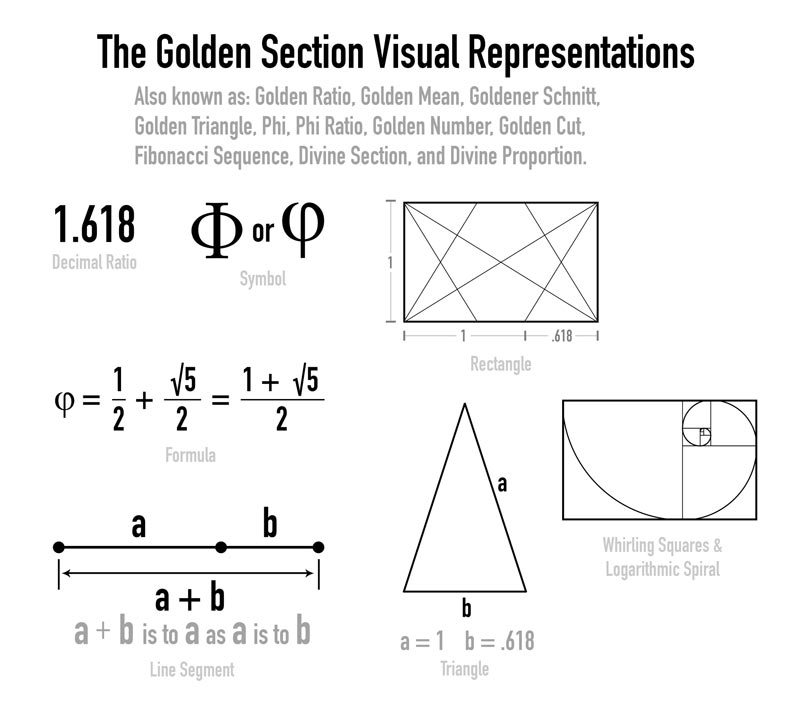
ONE
The logarithmic spiral of the phi rectangle is created by the arc within each square. This is something that is pretty obvious, especially if you’re familiar with the rectangle of the whirling squares, but the interesting thing is what we’ll see next.
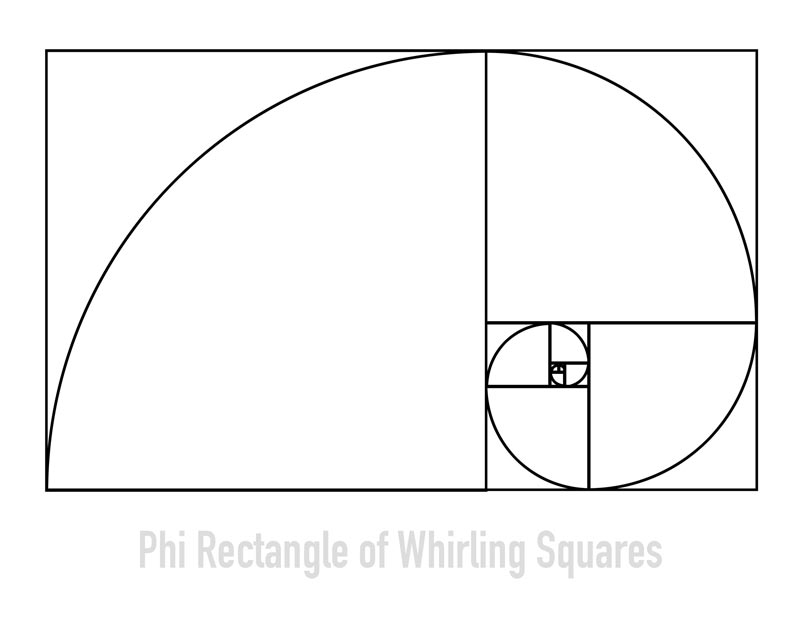
The arc in each square is 1/4 of a circle, so if we complete each circle we get an interesting design. Isn’t that cool?!
TWO
Out of all of the rectangles that are covered, the phi rectangle is the only one where the reciprocal is made and the other part of the rectangle makes a perfect square.
Remember the previous section where we learned about the reciprocal? We basically have a smaller phi rectangle rotated 90 degrees and inside the mother, which gives us a ratio of .618. If we subtract .618 from the phi ratio, we are left with one. And one equals a perfect square, which is shown on the right. The basic armature of the phi rectangle is seen on the left.
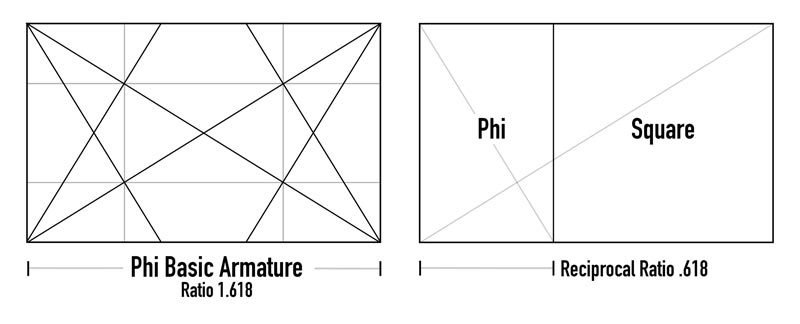
THREE
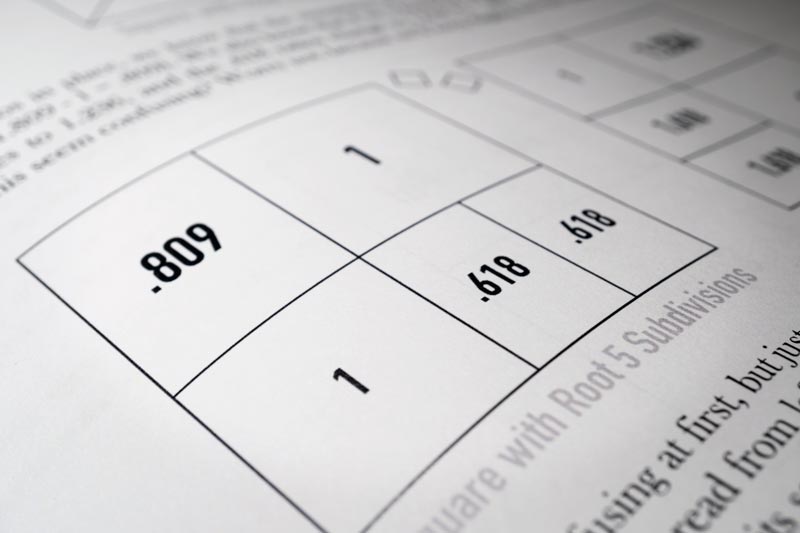
The root 5 rectangle has two reciprocal phi ratios and a square within it. This means it basically has two phi rectangles overlapping each other and sharing the square in the middle.
We can also see how the .618 shape rotates 90 dgrees to give us a rectangle with the phi ratio of 1.618. Same shape, but read differently as covered in the starting point.
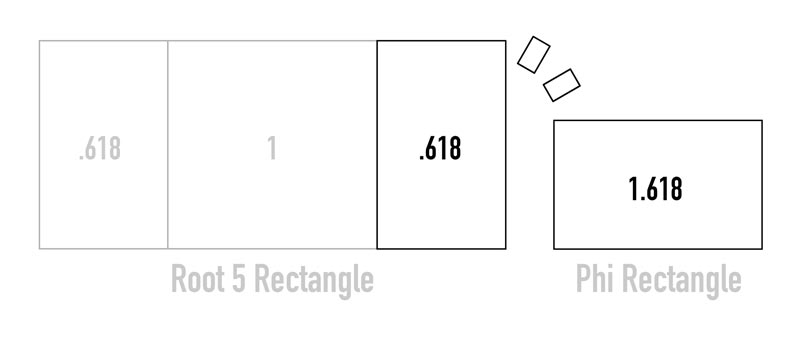
FOUR
As we also learned from the starting point, the rectangles are created by swinging a diagonal down from the square then completing the shape. Well, the phi rectangle is created by swinging a diagonal down from the center of the square instead of the corner. Aside from that, there’s something else to point out.
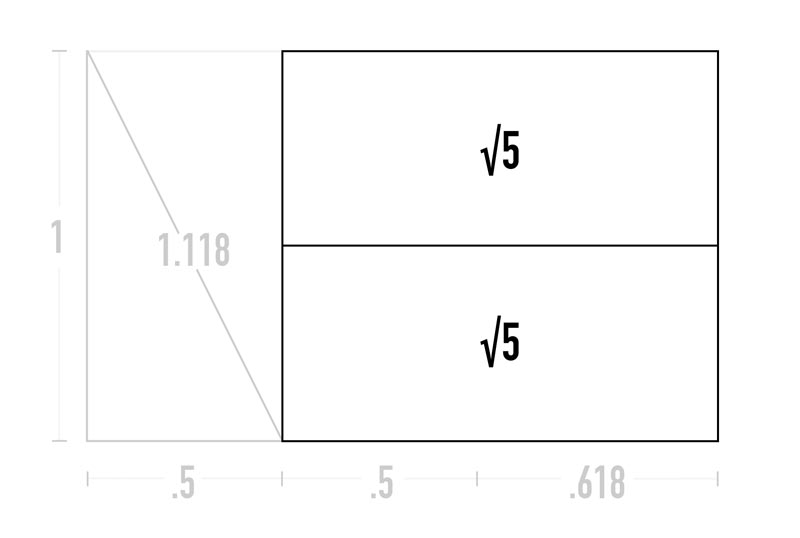
In the next diagram, we’ll see that .5 equals half of the square, so if the phi ratio is 1.618 and we subtract half of the square, that means the diagonal equals 1.118 (1.618 – .5 = 1.118). So why is this ratio significant?
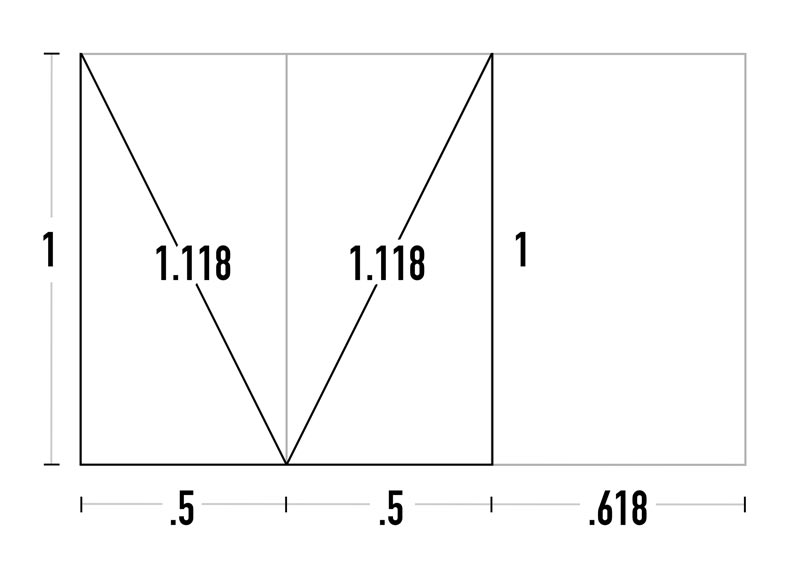
It’s the same exact ratio as two stacked root 5 rectangles! We can see this in the next example. Basically, when we stack a rectangle on top of another, we divide the ratio by two. So since the root 5 ratio is 2.236, we divide by 2 and get 1.118 (2.236 / 2 = 1.118). OK, so how does this relate to our phi rectangle again?
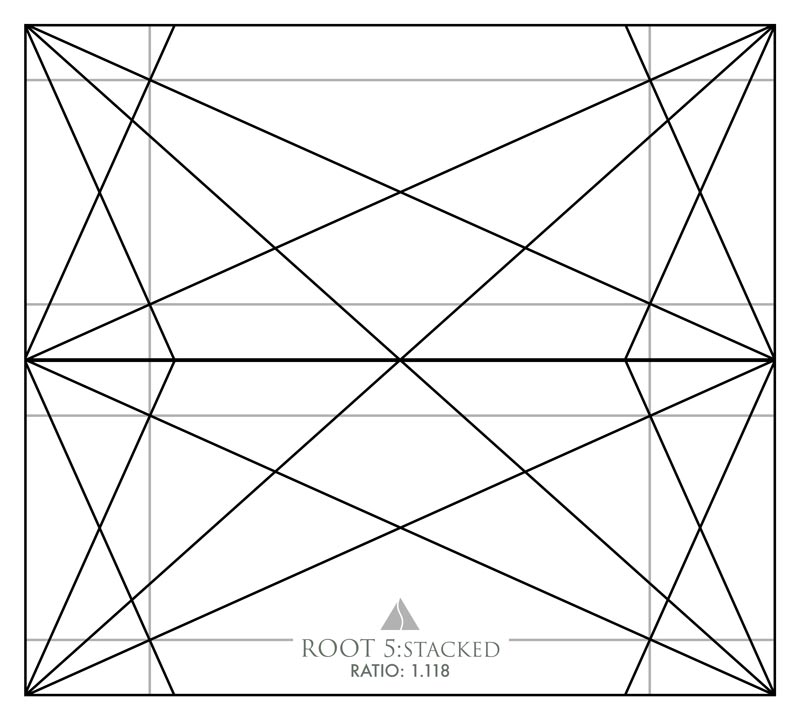
If we look back at our phi rectangle, we’ll now see that we have stacked root 5 rectangles on the right side. We are slowly learning how to subdivide the rectangles!
FIVE
The root phi rectangle is created from a phi rectangle. The interesting thing here, is that when we create a major diagonal within the root phi rectangle, we get two Kepler triangles.
What’s a Kepler triangle? Check out number six!
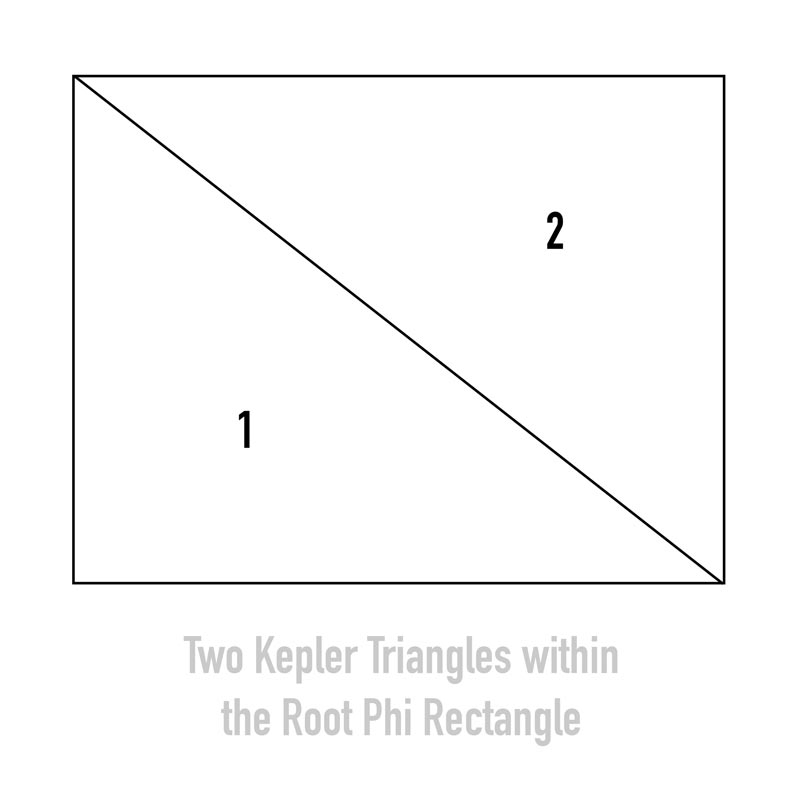
SIX
A mathematician and astronomer by the name of Johannes Kepler, first demonstrated the Kepler triangle, which relates to phi and the Pythagorean theorem. They are both covered in a visual way within the book, but for now, let’s just make note of this cool characteristic of phi.
To create the Kepler triangle and see how it relates to the Pythagorean theorem, we start with a triangle, where the bottom side, or “leg,” equals one. Then we make the right leg equal the ratio of the root phi, and the diagonal equal the ratio of phi. This gives us the Kepler triangle!
“Geometry has two great treasures: one is the theorem of Pythagoras, the other the division of a line into extreme and mean ratio. The first we may compare to a mass of gold, the second we may call a precious jewel.” Johannes Kepler

SEVEN
The reciprocal ratio of the root phi rectangle is .7861. When we make four of these side-by-side, then add them up, we get a length of 3.144 (.7861 x 4 = 3.144). This 3.144 ratio is known as JainPi, which is similar to the Pi ratio of 3.14.
Another interesting relationship with root phi and JainPi, is that they approximate one side of the pyramid’s base. Interesting, right?




Why the Ratios are Gold Dynamic Symmetry
Back to Summary
If you see a list full of ratios, you’ll never understand how they can be a tremendous help. That is, unless you’re shown why!
When flipping through Jay Hambidge’s book, you might’ve noticed that he’s got a lot of numbers listed. The new dynamic symmetry book has an even longer list of numbers, but it’s written with helpful aids to clue you in on their relationships to the grids.
At first glance, the ratios mean nothing and just add to the confusion. Yet, as you learn how to properly start, and learn about the reciprocal, you’ll eventually learn other cool dynamic symmetry related things. These include rectangle themes, overlapping rectangles, and compound rectangles…all which have different ratios. So how do we utilize the ratios?
Well, if you’re wanting to create a new phi sized canvas or fine art photo, but the diagonals of the phi rectangle don’t compliment the ones found in the environment and model, you can use a rectangle that is similar in shape but constructed with a different armature. Basically, you have more flexibility when you understand the ratio similarities.
Note: And if you don’t know why you should be concerned with the diagonals of the environment and model, don’t worry. We cover all of the techniques that are promoted by dynamic symmetry.
In the next example, we’ll see the ratio for the 4/3 rectangle which is a popular size of canvas and camera sensor. If the diagonals of the 4/3 rectangle armature aren’t complementing the environment or subject, there are other rectangles that are available which are similar or exact in size, but with different diagonals.
If the ratio for stacked root 7 rectangles is 1.323 and the 4/3 rectangle ratio is 1.333, then there is only a small difference in size. This means the root 7 rectangles can be used to compose the painting or photo and no one will “feel” or notice a difference.
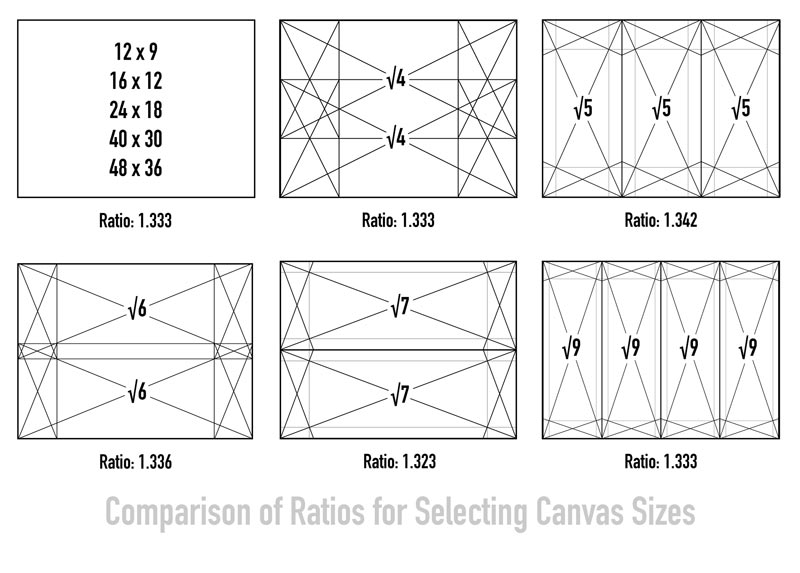
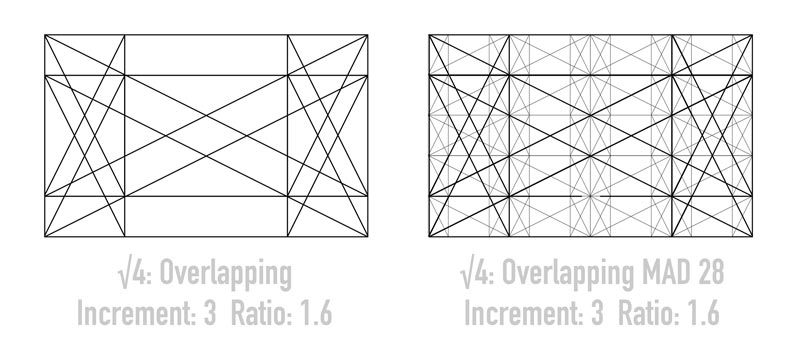
We’ve got several more ratios that are similar, and this next one named “Root 8: Overlapping MAD 112, Increment: 2” has a ratio of 1.616. That’s extremely close to the phi ratio of 1.618. That means we can use this grid configuration while still having a shape that looks like the phi rectangle.
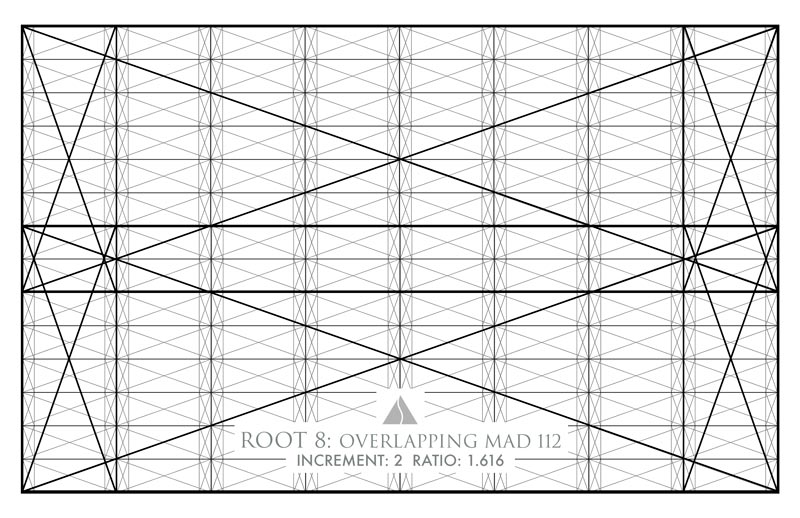
Just to see how flexible dynamic symmetry can be, here’s another grid variation “Root 4: Overlapping, Increment 3” which has a ratio of 1.6. This can also be used if needed, while still having the perceivable shape of the phi rectangle.
This slight variation in the ratios might drive mathematicians insane, but for us visual artists it allows us to be more flexible while still adhering to similar geometry found within the dynamic symmetry system.
Here’s another grid variation that can be used instead of the phi armature. This one is created with 4/3 rectangles and armature, with 6 on the bottom and 5 on the side…for a total of 30 within the 1.6 shape. Isn’t this flexibility great?
You’ll learn how to construct these grids to fit your needs, while also understanding how to find the ratio of each new shape.

I received an email, which refers to this ratio section:
“Tavis, I ran across and started watching your YouTube videos a few weeks ago. OUTSTANDING stuff!!!! I, like you, felt my photos were a bit lacking and your insight is taking me to another level. A couple of weeks ago I downloaded your eBooks and have enjoyed them a lot. Yesterday, I visited the NC Museum of Art and saw the master paintings in a very different light thanks to you.
My question is this, I primarily shoot a square medium-format camera. Can you give me some quick insight on the symmetry of the square photo? It seems to me to be inherently symmetrical and would just rely on the basic diagonals for composition.
Your insight would be really appreciated. Also, since square format is somewhat prominent in photography, possibly a video?
Thanks,
Charlie”
To answer Charlie’s great question, I pointed him towards looking at the ratios. If we know how to configure the root rectangles and understand the ratios, then we’ll be able to configure them to fit our needs.
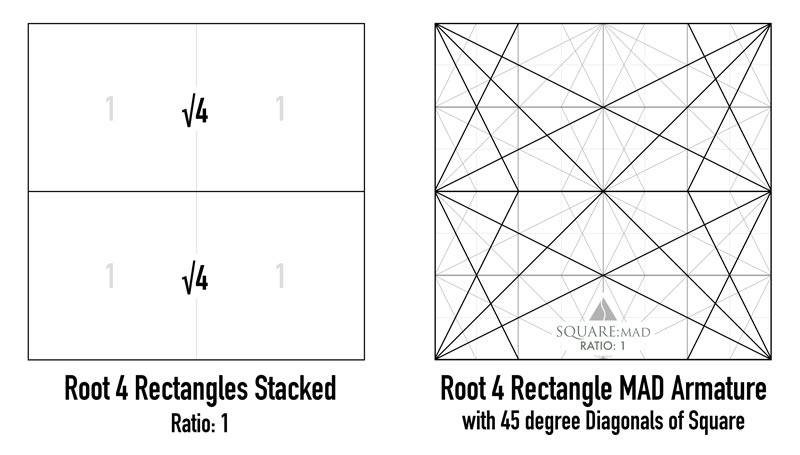
For the square composition, we have plenty of options. Referring to the ratio guide is the quickest thing we can do to figure out which grid configurations are possible for the square. In the next example, we see a section from the ratio guide. On the left side we see lots of ratios that are close to the ratio of one, so we have plenty of flexibility when composing an image in the square.
The root four rectangle is highlighted where we can read “Root 4….(mother rectangle, two stacked): 2 / 2 = 1).” So what does this mean?

This just gives us a visual clue of the grid configuration. It also gives us the simple arithmetic behind the configuration. So basically, we just stack one root 4 rectangle on top of the other. Since the ratio of the root 4 rectangle is two (two squares), we can stack them to make four smaller squares which equal one.
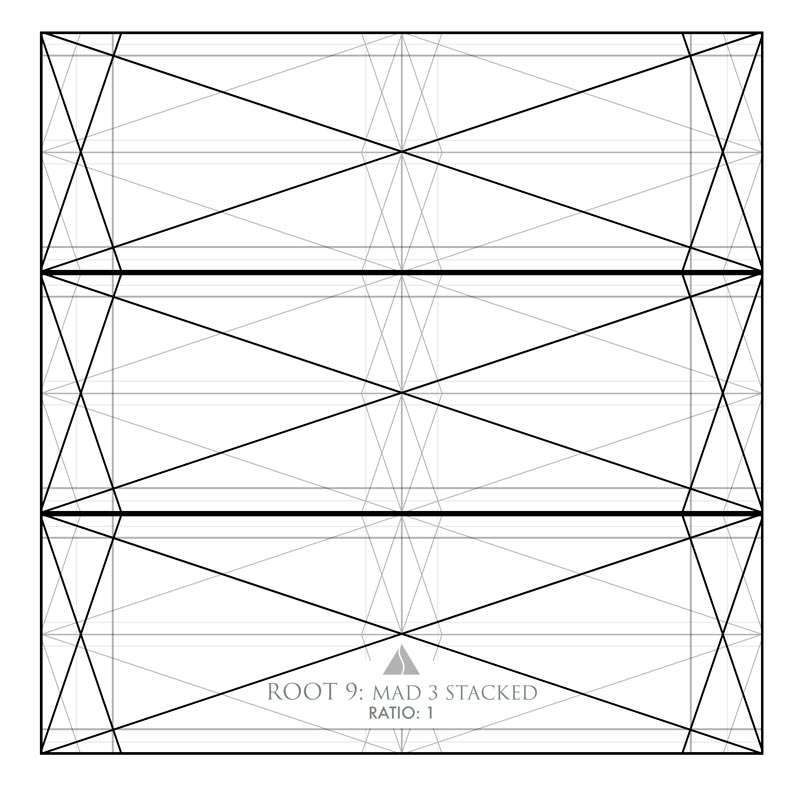
Here we can see how the root 9 rectangle, with a ratio of 3, can be stacked three times to equal a perfect square. The book goes into great detail of how we can configure the grids as we wish. It’s a fun game we can play, where we are in control of every move!

It’s essential to understand how to create your own grid variations, but if you don’t have the time then you can use dynamic symmetry grids that are already constructed. I’ve created over 240 grids, plus diagonal gauges for artists to use as tools for creating their next masterpiece. They will save you tons of time, and can be used on a computer, phone, iPad, or camera. They are also available to photographers through Adobe Lightroom and can be reorganized in Photoshop. Painters can print them out and use them to draw on a light pad.
To learn more about the dynamic symmetry grids, please follow the link below. You’ll learn more about dynamic symmetry books and see more applications of it in photography, cinema, and painting.


Table of Contents Dynamic Symmetry Book

Back to Summary
Here we have the complete table of contents, which will give you a great idea of the basic to advanced dynamic symmetry material. Use this book to understand and apply the same geometric mastery to your own artistic compositions.
Introduction
Chapter 1
Why We Need Dynamic Symmetry in Our Art
The Thing About Old Wives’ Tales
The Rule of Thirds: A Brief History
Chapter 2
The Golden Ratio and Dynamic Symmetry Timeline
Chapter 3
Applying Dynamic Symmetry Intuitively
Chapter 4
Demystifying the Grid
Chapter 5
Constructing the Root and Phi Rectangles
Constructing Non-Root Rectangles
Chapter 6
Understanding Rectangle Ratios
Chapter 7
Constructing the Basic Armature
The Reciprocal
Chapter 8
Square Compositions
Chapter 9
Breaking Down the Grids Further
Chapter 10
The Armature’s Polar Point
Chapter 11
Adding New Lines to Fit Our Needs

Chapter 12
Baroque vs Sinister Diagonal
Chapter 13
Building Grids Inside a Square
Chapter 14
Building Complex Designs Inside a Square
Chapter 15
Subdividing Shapes
Adding a Reciprocal
Subdivisions Within the Square
Subdividing with the Basic Armature
Compound Rectangle Nuances
Creating Compound Rectangles
Chapter 16
Overlapping Rectangles for Grid Variations
Other Helpful Overlapping Rectangles
Uneven Overlapping Divisions
Overlapping in a Linear Fashion

Chapter 17
Finding the Ratios of Overlapping Rectangles
More Configurations with Simple Math
Chapter 18
Rectangle Themes for Grid Variations
Theme “X”
Chapter 19
The Phi Ratio and More
The Pythagorean Theorem and Phi
The Root Phi Rectangle and Kepler Triangle
Building the Great Pyramid of Giza Without Math
Clearing Up Misconceptions About the Phi Ratio
How Masters Used Phi Calipers
Chapter 20
Techniques to Know Before Using the Grids
Gamut
Paralleling the Grid
Dominant Diagonal
90-Degree Angle
Coincidences
Negative Space and Filling the Grid
Figure-Ground Relationship
Starting with One Line
Chapter 21
Using Dynamic Symmetry in Drawing
Using a Light Pad to Assist with Drawing
Using Software to Assist with Drawing
Master Copies
Intricate Grid Designs

Chapter 22
Using Dynamic Symmetry in Painting
Squaring the Canvas to Transfer a Drawing
How to Draw Grids Onto the Canvas with Simple Math
Canvas Sizes Relating to the Grids
Chapter 23
Using Dynamic Symmetry in Sculpting
Chapter 24
Using Dynamic Symmetry in Cinematography
Chapter 25
Using Dynamic Symmetry in Fine Art Photography
Visualizing the Grid for Film Cameras
Chapter 26
Analyzing Art: A Muscle Memory Exercise
Finding the Rectangle by Using Ratios
Ratio Guide
Book Cover & Abstract Letters How I Designed the
Back to Summary
The book cover design was not traditional by any means, and it was inspired by the work of a master painters. I’ve created an entire article and video to show you what inspired me and exactly how I created each letter with dynamic symmetry. I also show you how I arranged the letters on the book cover by using dynamic symmetry and other design techniques. Click here or on the image below to check it out!


